Điều kiện biên
Theo phương pháp tuyến thì vector cảm ứng điện là liên tục ($\sigma_f = 0$), trong khi vector cường độ điện trường thì không (vì còn điện tích liên kết $\sigma_p$):
\[\begin{equation} D_{2n} - D_{1n} = \sigma_f \end{equation}\]Trong đó: $D_{2n}, \ D_{1n}$ lần lượt là vector cảm ứng điện tại môi trường $2$ và môi trường $1$, $\sigma_f$ là mật độ điện tích tự do.
\[\begin{equation} E_{2t} - E_{1t} = 0 \end{equation}\]Trong trường tĩnh điện, điện trường không đổi do đó $\nabla \times \mathbf{E} = 0$, ngược lại $\nabla \times \mathbf{D} = \nabla \times \mathbf{P}$ (có thể bằng $0$ hoặc khác $0$).
Tuy nhiên nếu dùng định lý Gauss cho vector điện trường:
\[\begin{equation} E_{2n} - E_{1n} = \sigma \end{equation}\]Thì lúc này, mật độ điện tích $\sigma = \sigma_f + \sigma_p$ bao gồm mật độ điện tích tự do và mật độ điện tích liên kết mặt.
Do đó ta thường sử dụng vector cảm ứng điện $\mathbf{D}$ nhằm dễ dàng tìm được vector điện trường $\mathbf{E}$, vì $\mathbf{D}$ pháp tuyến liên tục tại mặt phân cách, trong khi $\mathbf{E}$ thì không.
Một số câu hỏi thắc mắc và câu trả lời của mình
- Tại sao một điện tích điểm đặt trong điện môi thì điện trường bị giảm đi một hằng số điện môi
Khi đặt điện tích trong môi trường điện môi rộng vô hạn, khi đó điện tích gây ra một điện trường $\mathbf{E}$ khiến môi trường điện môi bị phân cực. Ta sẽ đi chứng minh điều này:
Sử dụng định lý Gauss cho vector cảm ứng điện, ta tìm được vector cảm ứng điện:
\[\begin{equation} \mathbf{D} = \frac{q}{4\pi r^2} \hat{r} \end{equation}\]Từ đây ta tìm được điện trường trong điện môi:
\[\begin{equation} \mathbf{E} = \frac{\mathbf{D}}{\epsilon} = \frac{q}{4\pi \epsilon r^2} \hat{r} \end{equation}\]Ta có công thức độ phân cực:
\[\begin{equation} \mathbf{P} = \mathbf{D} - \epsilon_0 \mathbf{E} = \frac{q}{4\pi}(\frac{\epsilon - \epsilon_0}{\epsilon}) \frac{\hat{r}}{r^2} \end{equation}\]Vậy mật độ điện tích khối lúc này là:
\[\begin{equation} \rho_p = -\nabla \cdot \mathbf{P} = \frac{q}{4\pi}(\frac{\epsilon - \epsilon_0}{\epsilon}) \nabla (\frac{\hat{r}}{r^2}) = -q(\frac{\epsilon - \epsilon_0}{\epsilon}) \delta^3(\mathbf{r}) \end{equation}\]Trong đó $\delta^3(\mathbf{r})$ là hàm Dirac Delta. Điều này bảo rằng mật độ điện tích khối $\rho_p$ chỉ có một điện tích điểm duy nhất và nó nằm duy nhất tại vị trí điện tích điểm $q$. Vậy điện môi bị phân cực tại bề mặt tiếp xúc với điện tích $q$ và trái dấu với điện tích.
Tổng điện tích lúc này bao gồm $Q = q + q_p = \frac{q}{\epsilon_r}$.
Lưu ý: Tổng các điện tích phân cực lúc này khác 0, vì chỉ có các điện tích trái dấu tại bề mặt tiếp xúc. Thế còn các điện tích phân cực dương đã đi đâu ? Chúng ở rìa của môi trường điện môi, tuy nhiên trong trường hợp này môi trường điện môi là vô hạn do đó các điện tích phân cực dương lúc này nằm ở vô cùng (do đó ta bỏ qua sự ảnh hưởng của chúng).
Ngược lại, nếu môi trường điện môi là hữu hạn thì ta không thể bỏ qua sự ảnh hưởng của các điện tích dương nằm ở rìa môi trường điện môi này. Nhìn vào chất điện môi của một tụ điện, ta thấy 2 rìa của chất điện môi bị phân cực với cùng điện tích và trái dấu nhau.
- Giả sử một quả cầu điện tích $Q > 0$ bán kính $a$, được bao quanh bởi một quả cầu điện môi đồng tâm bán kính $b > a$. Điện trường bên trong và bên ngoài quả cầu điện môi sẽ như nào ?
Khi này điện tích $Q$ gây ra điện trường làm phân cực điện môi, tuy nhiên quả cầu điện môi sẽ bị phân cực thành phần âm và phần dương (vì chất điện môi lúc này là hữu hạn). Phần âm tại bề mặt tiếp xúc với $Q$ và phân dương cùng độ lớn tại bề mặt quả cầu điện môi.
Lúc này điện trường bên trong điện môi bị giảm đi $\epsilon_r$ lần, vì chất điện môi lúc này bị phân cực thành âm và dương tạo ra một điện trường đều ngược hướng $\mathbf{E'}$ với điện trường $\mathbf{E_0}$ do $Q$ tạo ra, tổng hợp hai điện trường này:
\[\begin{equation} \mathbf{E}_{in} = \mathbf{E_0} + \mathbf{E'} = \frac{\mathbf{E_0}}{\epsilon_r} \end{equation}\]Điện trường bên ngoài chất điện môi lúc này giống như điện trường do điện tích gây ra bình thường:
\[\begin{equation} \mathbf{E}_{out} = \mathbf{E_0} \end{equation}\]Ta có thể dùng định lý Gauss cho điện trường để chứng minh điều này:
\[\begin{equation} \int \mathbf{E} \cdot d\mathbf{A} = \frac{Q_{total}}{\epsilon_0} = \frac{Q + Q_p}{\epsilon_0} \end{equation}\]Trong đó $Q_p$ là tổng các điện tích phân cực và nó bằng 0. Vậy điện trường lúc này giống như do điện tích $Q$ gây ra.
- Cùng cấu hình 2, Tại sao vừa ra khỏi điện môi thì điện trường lại tăng về như điện trường do điện tích $Q$ gây ra ? Thứ gì đã giúp tăng cường độ điện trường về như cũ ?
Hãy nhớ về vật dẫn (giả sử thay điện môi thành vật dẫn), tại sao trong vật dẫn điện trường bằng 0 nhưng ra khỏi vật dẫn thì lại có điện trường do điện tích $Q$ gây ra ? Đấy là vì trên bề mặt vật dẫn lúc này có các điện tích mặt (và nó bằng với điện tích $Q$).
Tương tự khi điện trường bị giảm trong điện môi, ngay khi chúng ra ngoài và được tăng thêm nhờ cường độ điện trường của các điện tích liên kết mặt bị phân cực tại bề mặt chất điện môi.
Chứng minh cấu hình ảnh điện trong điện môi
Cho một nửa môi trường vô hạn có chất điện môi $\epsilon_1$ và một nửa còn lại là $\epsilon_2$. Đặt một điện tích $q > 0$ vào môi trường chất điện môi $\epsilon_1$. Tìm cấu hình ảnh điện đối với trường hợp này.
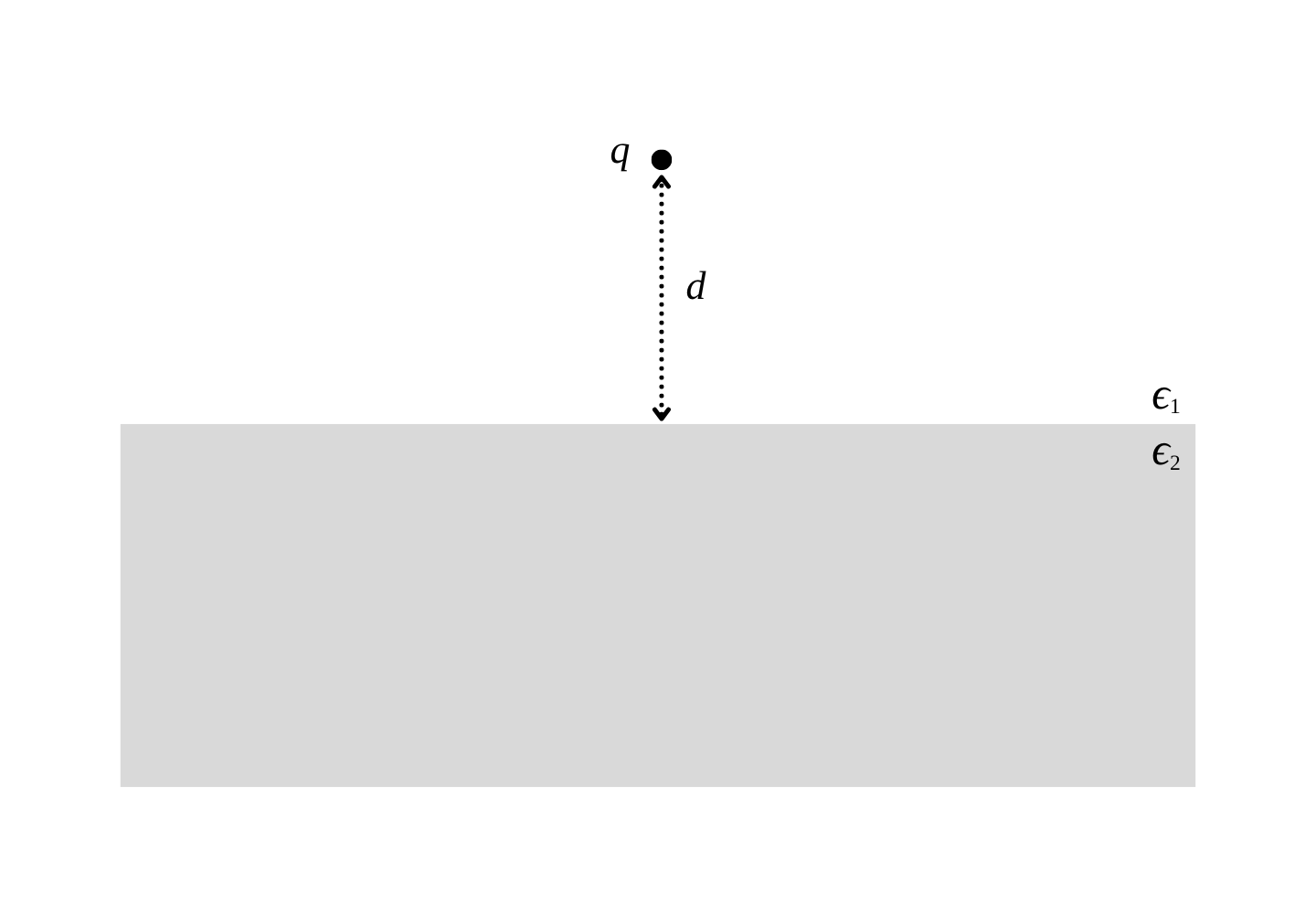
Điện tích $q$ làm phân cực chất điện môi $\epsilon_1$ và khiến điện trường bị giảm đi $\epsilon_1$ lần. Tại bề mặt phân cách trong môi trường $\epsilon_1$ xuất hiện các điện tích liên kết mặt $\sigma_1$ và bên môi trường $\epsilon_2$ là $\sigma_2$.
Ta có điện tích liên kết mặt tại mặt phân cách là $\sigma = \sigma_1 + \sigma_2$. Ta xem mặt phân cách như là một mặt phẳng tích điện, và nó gây ra một điện trường vuông góc với mặt phân cách:
\[E^1_{Oz} = \frac{\sigma}{2\epsilon_0}\] \[E^2_{Oz} = -\frac{\sigma}{2\epsilon_0}\]Tại mặt phân cách, ta có điều kiện biên:
\[\begin{equation*} D_{2n} - D_{1n} = \sigma_f = 0 \rightarrow D_{1n} = D_{2n} \end{equation*}\]Hay:
\[\epsilon_0 \epsilon_1 E_{1n} = \epsilon_0 \epsilon_2 E_{2n}\] \[\rightarrow \epsilon_1 (\frac{\sigma}{2\epsilon_0} - \frac{q}{4\pi \epsilon_0 \epsilon_1 r^2} cos \ \theta) = \epsilon_2 (-\frac{\sigma}{2\epsilon_0} - \frac{q}{4\pi \epsilon_0 \epsilon_1 r^2} cos \ \theta) \\\] \[\rightarrow \sigma = \frac{q cos \ \theta}{2 \pi \epsilon_1 r^2} (\frac{\epsilon_1 - \epsilon_2}{\epsilon_1 + \epsilon_2})\]
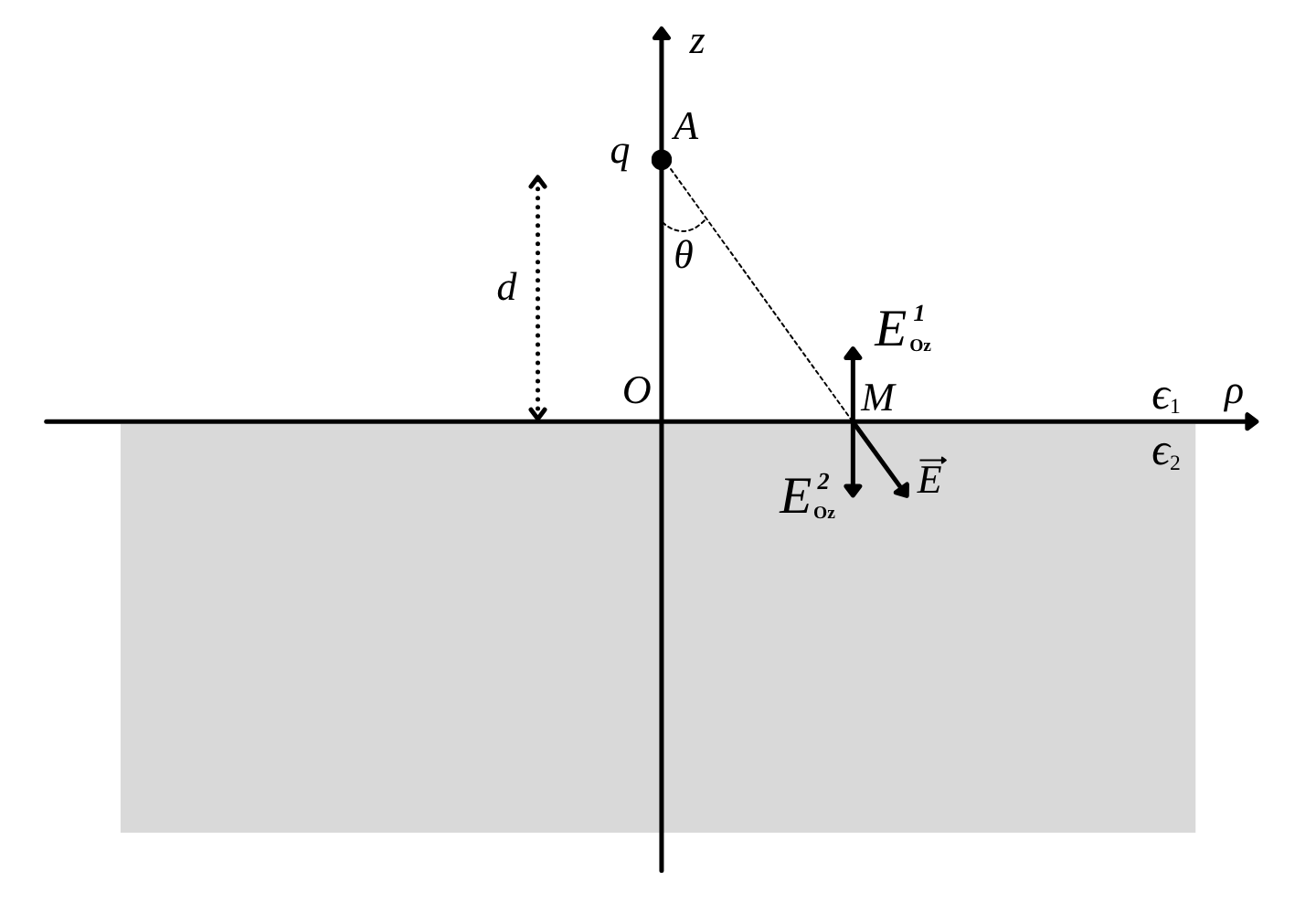
Hay ta còn có thể viết lại:
\[\sigma (\theta) = \frac{q \ cos^3 \ \theta}{2 \pi \epsilon_1 d^2} (\frac{\epsilon_1 - \epsilon_2}{\epsilon_1 + \epsilon_2})\]Đặt:
\[q_1 = (\frac{\epsilon_1 - \epsilon_2}{\epsilon_1 + \epsilon_2}) \frac{q}{\epsilon_1}\] \[\sigma (\theta) = \frac{q_1}{2 \pi d^2} \ cos^3 \ \theta\]Xét điểm $M_1(z, 0)$. Điện thế tại $M_1$ do điện tích $q/\epsilon_1$ và điện tích liên kết $\sigma (\theta)$ trên mặt phân cách gây ra là:
\[V_{M_1} = \frac{1}{4 \pi \epsilon_0} \frac{q}{\epsilon_1 | z - d|} + V_{\sigma}\]Trong đó $V_\sigma$ là điện thế do điện tích liên kết tại mặt phân cách $dq$ gây ra, ta có thể tính $dq = \sigma \cdot da$ và để đơn giản ta dùng hệ tọa độ cực $(\rho, \phi)$ nên $da = \rho d\rho \cdot d \phi$. Từ đó ta tính được $dq = \sigma \cdot \rho d\rho \cdot d\phi$:
\[\begin{equation*} \begin{aligned} V_{\sigma} &= \int dV = \int^{2\pi}_0 \int^\infty_0 \frac{1}{4\pi \epsilon_0} \frac{\sigma \rho \ d\rho \cdot d\phi}{\sqrt{\rho^2 + z^2}} \\ &= \int^\infty_0 \frac{1}{4\pi \epsilon_0} \frac{\sigma 2\pi \rho \ d\rho}{\sqrt{\rho^2 + z^2}} \end{aligned} \end{equation*}\]Ta có: $\rho/d = tan \ \theta \rightarrow \rho = d \cdot tan \ \theta$ và $d\rho = d \cdot d\theta / cos^2 \ \theta$.
\[\begin{equation*} \begin{aligned} V_{\sigma} &= \frac{q_1}{4 \pi \epsilon_0} \int^{\pi/2}_0 \frac{cos^3 \theta \cdot sin \theta \cdot d\theta}{cos^2 \theta \cdot cos \theta \cdot \sqrt{d^2 tan^2 \theta + z^2}} \\ &= \frac{q_1}{4 \pi \epsilon_0} \int^{\pi/2}_0 \frac{sin \theta \cdot cos \theta \cdot d\theta}{\sqrt{d^2 sin^2 \theta + z^2 cos^2 \theta}} \\ \end{aligned} \end{equation*}\]Đặt:
\[u = d^2 sin^2 \theta + z^2 cos^2 \theta \\ \rightarrow du = (2d^2sin\theta \cdot cos \theta - 2z^2 cos \theta \cdot sin\theta)d\theta = 2(d^2 - z^2) cos\theta \cdot sin \theta d\theta\]Khi $\theta = 0 \rightarrow u = z^2$
Khi $\theta = \pi/2 \rightarrow u = d^2$
\[\begin{align*} V_{\sigma} &= \frac{q_1}{4 \pi \epsilon_0 (d^2 - z^2)} \int^{d^2}_{z^2} \frac{du}{2\sqrt{u}} \\ &= \frac{q_1}{4 \pi \epsilon_0} \frac{d - z}{d^2 - z^2} \\ &= \frac{q_1}{4\pi \epsilon_0 (d + z)} \\ &= \frac{q'}{4\pi \epsilon_0 \epsilon_1 (d + z)} \end{align*}\]Trong đó ta đặt $q' = \epsilon_1q_1 = (\dfrac{\epsilon_1 - \epsilon_2}{\epsilon_1 + \epsilon_2})q$. Vậy điện thế do các điện tích liên kết tại mặt phân cách gây ra tương đương như điện thế do điện tích $q'$ đặt tại $(-d, 0)$ trong môi trường $\epsilon_1$ gây ra:
\[V_{M_1} = \frac{1}{4 \pi \epsilon_0} \frac{q}{\epsilon_1 | z - d|} + \frac{1}{4 \pi \epsilon_0} \frac{q'}{\epsilon_1 (d + z)}\]Chứng minh tương tự đối với một điểm $M_2(z, 0)$ $(z < 0)$ trong môi trường $\epsilon_2$:
\[\begin{align*} V_{M_2} &= \frac{1}{4 \pi \epsilon_0} \frac{q}{\epsilon_1 (d - z)} + V_{\sigma} \\ &= \frac{1}{4 \pi \epsilon_0} \frac{q}{\epsilon_1 (d-z)} + \frac{q'}{4 \pi \epsilon_0 \epsilon_1 (d - z)} \\ &= \frac{1}{4 \pi \epsilon_0} \frac{q''}{\epsilon_2 (d-z)} \end{align*}\]Trong đó $q'' = \dfrac{2\epsilon_2}{\epsilon_2 + \epsilon_1} q$ đặt tại $A(d, 0)$ trong môi trường $\epsilon_2$.
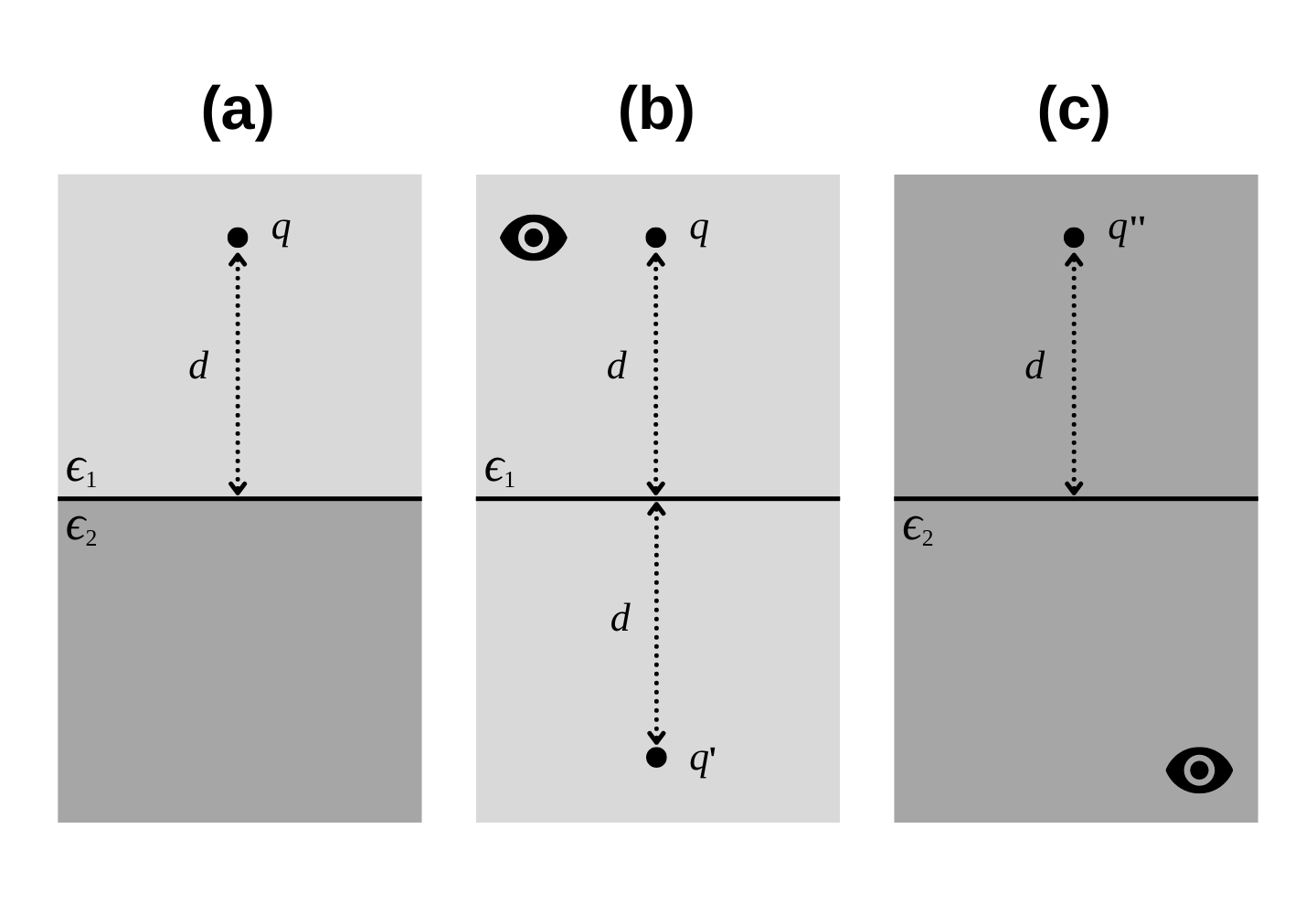
Hình $(a)$, là cấu hình ban đầu của bài toán.
Hình $(b)$, là điện trường do điện tích $q$ và điện tích liên kết tại mặt phân cách gây ra trong môi trường $\epsilon_1$ ($z > 0$) tương đương như điện trường do hệ điện tích $q$ tại $A(d, 0)$ và $q'$ tại $A'(-d, 0)$ đặt đối xứng qua mặt phân cách trong cùng một môi trường $\epsilon_1$.
Hình $(c)$, là điện trường do điện tích $q$ và điện tích liên kết tại mặt phân cách gây ra trong môi trường $\epsilon_2$ ($z < 0$) tương đương như một điện tích $q''$ đặt trong môi trường $\epsilon_2$ tại $A(d, 0)$.
Như vậy, do điện trường không liên tục tại mặt phân cách nên ta không thể xây dựng một hàm điện trường chỉ với một cấu hình ảnh điện duy nhất được. Ta phải phân ra hai cấu hình ảnh điện cho điện trường trong từng môi trường $\epsilon_1$ và $\epsilon_2$.