Giới thiệu vấn đề nghiên cứu
Đã bao giờ bạn tự hỏi, trực thăng bay lên như nào hay chưa ? Trực thăng bay lên được là nhờ các cánh quạt quay, tạo ra một lực $F$ tác dụng vào không khí hướng xuống, đồng thời theo định luật $III$ Newton không khí cũng tạo ra một phản lực $F$ tác dụng vào trực thăng hướng lên.
Hay giải thích theo cách khác là do sự chênh lệch áp suất phía trên và phía dưới cánh quạt gây ra. Cánh quạt của trực thăng quay với tốc độ cao, tạo ra một dòng khí chuyển động tương đối với không khí. Theo nguyên lý Bernoulli dòng khí này tạo ra áp suất thấp ở mặt trên của cánh quạt và áp suất cao ở mặt dưới của cánh quạt. Sự chênh lệch áp suất này tạo ra lực nâng, giúp trực thăng bay lên.
Do đó cánh trực thăng thường bị cong lên một tí, nhằm gia tăng lực nâng cho trực thăng. Từ đó, khi trực thăng đứng yên ở trên không thì lực nâng sẽ cân bằng với trọng lực.
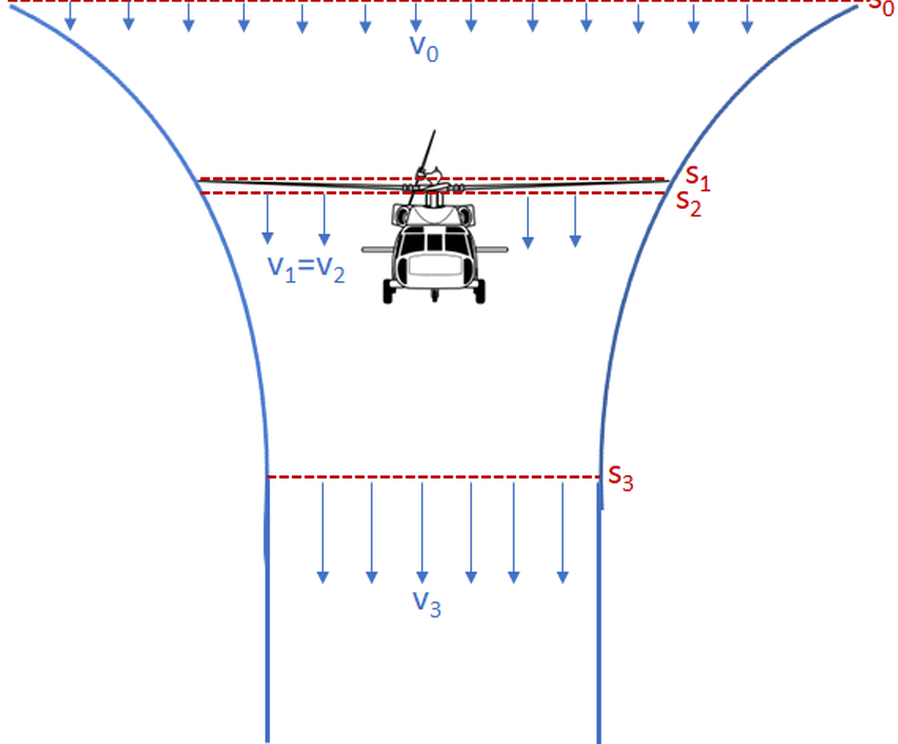
spinningwing.com/the-helicopter/momentum-theory
Thế câu hỏi đặt ra là trực thăng sẽ tiêu thụ công suất nhiều hơn khi đứng yên ở trên không hay là khi di chuyển tịnh tiến về phía trước ? Hay nói một cách đơn giản hơn, hãy giải thích định tính hàm $P(v)$ với $P$ là công suất tiêu thụ và $v$ là vận tốc tịnh tiến. Bên dưới là đồ thị $P(v)$ khi được thực nghiệm trong thực tế:
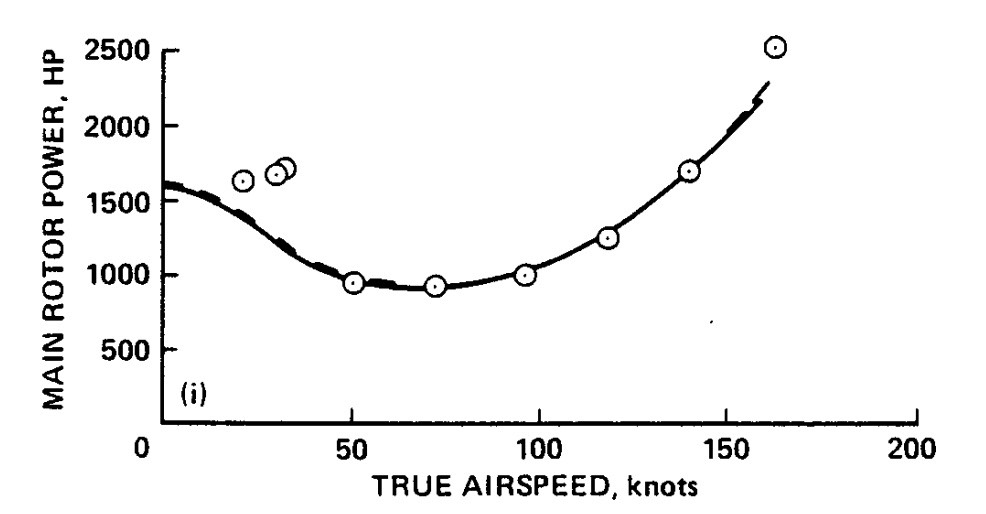
NASA Technical Memorandum 88360, Fig. B1
Lực đẩy của một động cơ
Thứ nguyên của lực: $[F] = MLT^{-2}$
Trên thực tế, ta ước lượng rằng lực đẩy của động cơ phụ thuộc vào các yếu tố như diện tích cánh quạt, tần số góc của cánh quạt, mật độ không khí:
\[F_{thrust} \propto C \times A^{\alpha}\omega^{\beta}{\rho_{air}}^{\gamma}\]Phân tích thứ nguyên ta được:
\[MLT^{-2} = C \times (L^2)^{\alpha} \times (T^{-1})^{\beta} \times (ML^{-3})^{\gamma}\]Cân bằng thứ nguyên và giải hệ phương trình 3 ẩn:
Thứ nguyên $[M]$: $M = M^{\gamma}$
Thứ nguyên $[L]$: $L = L^{2\alpha \ - \ 3\gamma}$
Thứ nguyên $[T]$: $T^{-2} = T^{-\beta}$
Từ đó ta tìm được các hệ số như sau:
\[\alpha = 2, \ \beta = 2, \ \gamma = 1 \\ \rightarrow F_{thrust} \propto C \times A^2\omega^2{\rho_{air}}\]Hay ta còn có thể viết lại như sau:
\[F_{thrust} \propto C \times Av^2{\rho_{air}}\]Với $v$ là vận tốc dài của động cơ và $C$ là một hằng số.
Hằng số $C$ không thể tìm được bằng phương pháp phân tích thứ nguyên. Đây cũng chính là nhược điểm của phương pháp này, tuy nhiên phương pháp thứ nguyên lại rất hữu ích trong việc ước lượng công thức nhanh chóng.
Bằng việc giải các phương trình khác ta tìm được hằng số $C = 1/2 \times C_T$ với $C_T$ là hằng số đẩy.
Và đây chính là công thức tính lực đẩy của mỗi động cơ mà ta cần tìm:
\[F_{thrust} = \frac{1}{2} Av^2{\rho_{air}}C_T\]Công suất tiêu thụ
Trực thăng đứng yên
Để trực thăng lơ lửng giữa không trung thì lực đẩy của động cơ phải cân bằng với trọng lực:
\[\begin{equation*} \begin{aligned} & F_{thrust} = P \\ \rightarrow \ & \frac{1}{2} Av^2 \rho_{air} C_T = mg \\ \rightarrow \ & v = \sqrt{\frac{2mg}{\rho_{air} C_TA}} \end{aligned} \end{equation*}\]Công suất để giữ trực thăng đứng yên là:
\[\begin{equation*} \begin{aligned} P & = F_{thrust} \times v \\ & = mg \times \sqrt{\frac{2mg}{\rho_{air} C_TA}} \\ & = \sqrt{\frac{2(mg)^3}{\rho_{air} C_TA}} \end{aligned} \end{equation*}\]Từ công thức ta dễ dàng đánh giá được công suất tỉ lệ với khối lượng $P \sim m^{3/2}$
Trực thăng chuyển động thẳng đều
Khi trực thăng chuyển động, lúc này mọi chuyện sẽ khác và phức tạp hơn rất nhiều.
Khi trực thăng di chuyển sẽ gây ra một lực cản cảm ứng (induced drag) tỉ lệ với $1/v^2$. Lực cản cảm ứng (induced drag) thực chất không phải là một loại lực ma sát mà là một hệ quả của việc tạo ra lực nâng, lực cản cảm ứng (induced drag) khá phức tạp vì nó liên quan đến khí động lực học, do đó ta sẽ không đi sâu vào lực cản này. Bạn có thể tìm hiểu thêm Prandtl’s lifting line theory.
Bên cạnh đó, việc di chuyển với vận tốc không đổi cũng gây ra một lực cản của không khí (parasitic drag) tỉ lệ với $v^2$.
Lúc này, trực thăng sẽ có công suất tiêu thụ là tổng của công suất do lực cản cảm ứng và lực cản không khí gây ra.
\[P_{total} = P_{induced} + P_{parasitic}\]Ta ước lượng rằng, lực cản không khí (parasitic drag) phụ thuộc vào diện tích, mật độ không khí, vận tốc:
\[\begin{equation*} \begin{aligned} & F_{parasitic} \propto \frac{1}{2} Av^2{\rho_{air}} \\ \rightarrow \ & P_{parasitic} = F_{parasitic} \times v = \frac{1}{2} Av^3{\rho_{air}} \\ \rightarrow \ & P_{parasitic} \sim v^3 \end{aligned} \end{equation*}\]Riêng lực cản cảm ứng (induced drag) ta sẽ tìm được như sau:
\[\begin{equation*} \begin{aligned} & F_{induced} = \frac{(mg)^2}{.5 \times Av^2\rho_{air}} \\ \rightarrow \ & P_{induced} = F_{induced} \times v = \frac{(mg)^2}{.5 \times Av\rho_{air}} \\ \rightarrow \ & P_{induced} \sim \frac{1}{v} \end{aligned} \end{equation*}\]Vậy công suất tiêu thụ của trực thăng là:
\[P_{total} \propto \frac{\alpha}{v} + \beta v^3\]Trong đó $\alpha, \ \beta$ là các hằng số.
Đồ thị của công suất sẽ có dạng như sau:
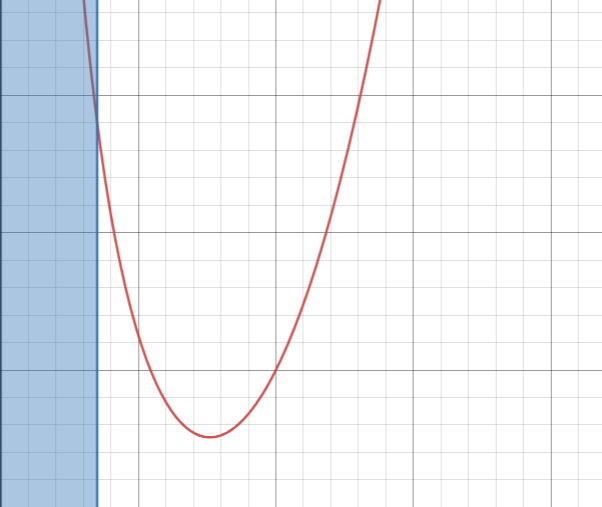
Phần màu xanh là khi máy bay đứng yên.
Để tìm vận tốc mà tại đó công suất tiêu thụ là nhỏ nhất thì ta cần giải phương trình sau:
\[\begin{equation*} \begin{aligned} & \frac{dP_{total}}{dv} = \frac{d}{dv}(\frac{\alpha}{v} + \beta v^3) = 0 \\ \leftrightarrow \ & -\frac{\alpha}{v^2} + \beta v^2 = 0 \\ \leftrightarrow \ & v = \sqrt[4]{\frac{\alpha}{\beta}} \\ \end{aligned} \end{equation*}\]Kết luận
Ta đã vừa giải thích một cách định tính cho đồ thị $P(v)$ ở đầu bài viết, tuy nhiên đây chắc chắn không thực sự chính xác vì ta đã bỏ qua một số công suất khác cũng quan trọng không kém.
Về cơ bản ta đã sử dụng phương pháp thứ nguyên để ước lượng các công thức, từ đây ta thấy phương pháp thứ nguyên thực sự rất quan trọng trong Vật Lý. Tuy nhiên theo tác giả hiện nay, có vẻ chương trình Vật Lý ở trường học khá xem nhẹ phương pháp này và thậm chí là bỏ qua (có lẽ là tưởng rằng nó vô dụng).
Tuy nhiên như ta đã thấy nó rất hữu ích trong việc ước lượng công thức và kiểm tra tính đúng đắn của công thức hoặc một kết quả nào đó.