1. Phát biểu vấn đề nghiên cứu
Giả sử ta có một chiếc cốc bán kính $R$ cao vô hạn, có nước bên trong cốc và độ cao mực nước ban đầu là $L$. Bây giờ ta nghiêng chiếc cốc một góc $0 \leq \theta \leq \pi/2$ bất kì, thì mực nước trong cốc lúc bấy giờ sẽ thay đổi như nào ? Hãy đi tìm hàm $h(\theta)$ đó.
2. Giải quyết vấn đề
2.1. Mô hình đơn giản
Để đơn giản hóa trong việc tính toán, ở mô hình đơn giản này ta sẽ giả sử chiếc cốc là một hình hộp chữ nhật. Ta sẽ chia ra 2 trường hợp: $\theta \geq \theta_0$ và $\theta \leq \theta_0$.
Thế $\theta_0$ ở đây là gì ? $\theta_0$ ở đây là góc hợp giữa cốc và mặt phẳng ngang mà khi đó là giao của sự chuyển đổi hình dạng của nước từ "hình thang" sang "hình tam giác" (khi nhìn cốc nước theo hướng bên).
Ta dễ dàng tìm được $\theta_0 = arctan(\frac{L}{R})$, ta sẽ đi giải quyết trường hợp đầu tiên $\theta \geq \theta_0$ (hình dạng của nước lúc này là hình thang hoặc là tam giác nếu $\theta = \theta_0$).
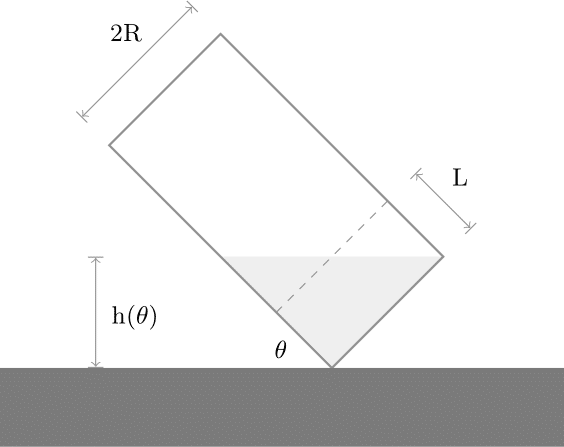
Như hình vẽ, ta dễ dàng thấy phần diện tích ở phía trên đã di chuyển xuống phần diện tích ở dưới. Ta đơn giản tìm được độ cao mực nước lúc này là:
\[h(\theta) = Lsin(\theta) + Rcos(\theta)\]Tiếp đến là trường hợp $\theta \leq \theta_0$, hình dạng của nước lúc này là hình tam giác:
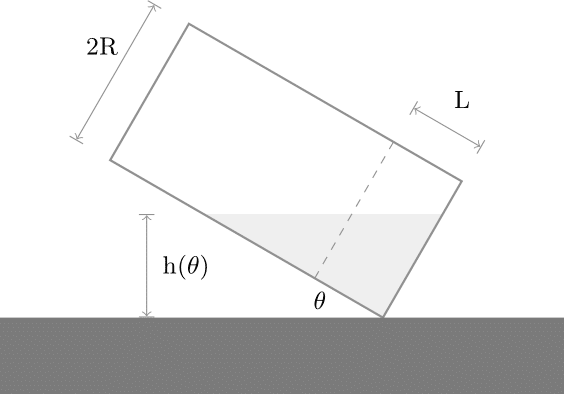
Lúc này ta sẽ giải quyết vấn đề khác với trường hợp đầu. Ta thấy rằng cho dù cốc nước nghiêng với một góc như thế đi nữa thì thể tích của nước là không đổi. Ta có điều kiện $V_0 = V$ hay $A_0 = A$ với $A$ là diện tích của nước (vì độ dày là bằng nhau).
Ta dễ dàng tìm được diện tích của nước như sau:
\[A(\theta) =\frac{1}{2}\frac{h(\theta)}{sin(\theta)}\frac{h(\theta)}{cos(\theta)}\]Do thể tích nước là bảo toàn nên ta có (gọi bề dày là $a$):
\[\begin{equation*} \begin{aligned} & V(\theta) = V_0 \leftrightarrow aA(\theta) = aA_0 \\ & \leftrightarrow \frac{1}{2}\frac{h(\theta)}{sin(\theta)}\frac{h(\theta)}{cos(\theta)} = 2LR \\ & \leftrightarrow h(\theta) = \sqrt{4LRsin(\theta)cos(\theta)} \end{aligned} \end{equation*}\]Tổng kết lại chúng ta có được hàm độ cao mực nước phụ thuộc vào góc $\theta$ như sau (đây là một hàm liên tục):
\[\begin{equation*} h(\theta) = \begin{cases} Rcos(\theta) + Lsin(\theta) & \theta \geq \theta_0 \\ \sqrt{4LRsin(\theta)cos(\theta)} & \theta \leq \theta_0 \end{cases} \end{equation*}\]Việc cần giải quyết vấn đề ở mô hình đơn giản này nhằm đơn giản hóa tính toán và hiểu được hướng giải quyết của vấn đề. Từ đó giải quyết mô hình phức tạp dễ dàng hơn.
2.2. Mô hình phức tạp
Tuy mô hình trên khá đơn giản, nhưng trên thực tế các cốc nước đều có dạng là hình trụ, do đó vấn đề sẽ phức tạp hơn rất nhiều. Tương tự, ta chia ra 2 trường hợp là $\theta \geq \theta_0$ và $\theta \leq \theta_0$.
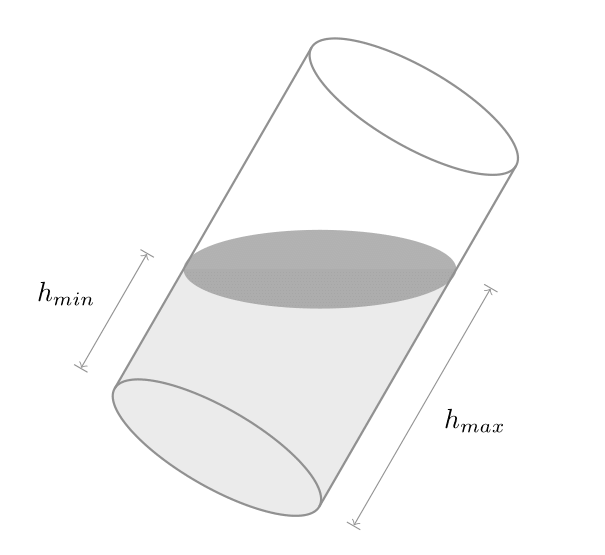
Ở trường hợp $\theta \geq \theta_0$ đơn giản ta chỉ cần tính thể tích của hình phiến trụ. Ta đã biết rằng, thể tích hình phiến trụ là:
\[V(\theta) = \frac{\pi R^2 (h_{min} + h_{max})}{2}\]Từ hình vẽ, ta tìm được:
\[\begin{equation*} \begin{aligned} & h_{max} = \frac{h(\theta)}{sin(\theta)} \\ & h_{min} = h_{max} - \frac{2R}{tan(\theta)} \end{aligned} \end{equation*}\]Do thể tích nước là bảo toàn nên ta có:
\[\begin{equation*} \begin{aligned} & V(\theta) = V_0 \\ & \leftrightarrow \frac{\pi R^2 (2h_{max} - 2R/tan(\theta))}{2} = L \pi R^2 \\ & \leftrightarrow L = h_{max} - \frac{R}{tan(\theta)} \\ & \leftrightarrow \frac{h(\theta)}{sin(\theta)} = L + \frac{Rcos(\theta)}{sin(\theta)} \\ & \leftrightarrow h(\theta) = Lsin(\theta) + Rcos(\theta) \end{aligned} \end{equation*}\]Và chúng ta tìm được hàm $h(\theta)$ hoàn toàn giống như ở mô hình đầu tiên.
Riêng trường hợp $\theta \leq \theta_0$ thì lại phức tạp hơn rất nhiều. Lúc này ta sẽ cần dùng đến vi tích phân để tính thể tích nước trong cốc.
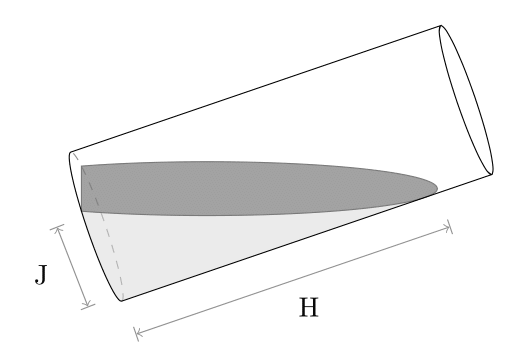
Chọn trục tọa độ như hình vẽ với tâm $O$ là tâm của hình tròn bán kính $R$. Đầu tiên ta chia nhỏ thể tích nước thành các hình chữ nhật như sau:
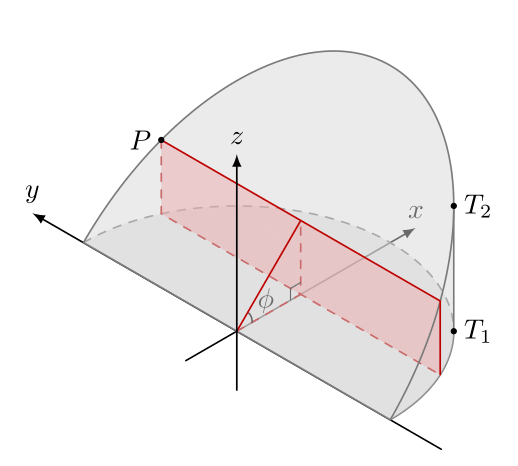
Gọi $J, H$ lần lượt độ dài của phần nước ở đáy cốc và độ dài cạnh góc vuông lúc này, ta tính được các đại lượng sau:
\[\begin{aligned} & \phi = \pi/2 - \theta \\ & z(x) = \frac{H(x - R + J)}{J} \\ & y(x) = \sqrt{R^2 - x^2} \end{aligned}\]Và diện tích phần hình chữ nhật lúc này là:
\[A(x) = z(x) \times 2y(x)\]Từ đó ta lấy tổng tất cả các hình chữ nhật bằng cách tích phân cận từ $(R - J) \rightarrow R$, ta được:
\[\begin{equation*} \begin{aligned} V(\theta) & = \int_{R - J}^{R} A(x) dx \\ &= 2\int_{R - J}^{R} \frac{H(x - R + J)}{J} \times \sqrt{R^2 - x^2} \ dx \\ &= \frac{H\times R^2}{3}(\frac{3sin(\psi) - 3 \psi cos(\psi) - sin^3(\psi)}{1 - cos(\psi)}) \end{aligned} \end{equation*}\]Với:
\[\displaylines{\psi = \pi - arctan(\frac{J - R}{R})\\ H = \frac{h(\theta)}{sin(\theta)}, \ J = \frac{h(\theta)}{cos(\theta)}}\]Tương tự, do thể tích nước trong cốc nước bảo toàn nên ta có:
\[V(\theta) = V_0 = L\pi R^2\]Giải phương trình trên và ta sẽ tìm được $h(\theta)$.
2.3. Biện luận và thử nghiệm
Từ các công thức trên, ta thấy rằng khi góc $\theta \rightarrow 0$ thì $H \rightarrow \infty$ và $J \rightarrow 0$
Để dễ hình dung mực nước di chuyển như nào, ta cần vẽ đồ thị $h(\theta)$.
Ở đây ta thử nghiệm với $L = R = 1.5$, Bên dưới là bảng dữ liệu mà tác giả đã tính toán được đối với trường hợp $\theta \leq \theta_0$:
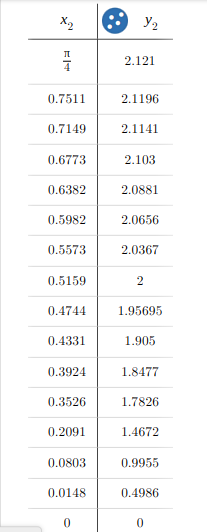
Ta dễ thấy $y_2$ ban đầu giảm rất chậm, sau đấy thì lại giảm càng nhanh và dốc hơn rất nhiều. Tác giả dự đoán rằng đây là một hàm lũy thừa:
\[f(x) = a \times x^b\]Thật vậy, từ việc dùng Nonlinear Regression, ta có được đồ thị của mực nước lúc đấy như sau:
\[h(\theta) \approx 2.41978 \times \theta^{0.328745}\]Bên dưới là đồ thị kết hợp cả 2 trường hợp:
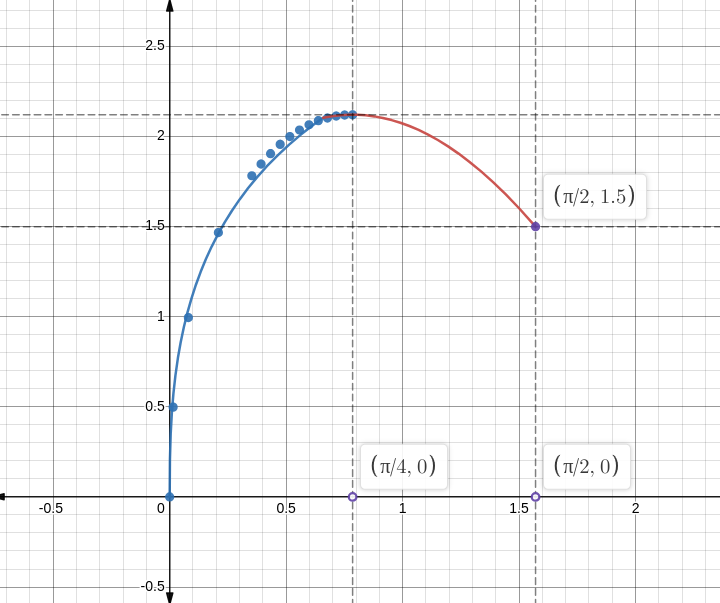
Phần màu đỏ là trường hợp $\theta \geq \theta_0$ (hình phiến trụ) và phần màu xanh là trường hợp $\theta \leq \theta_0$ (hình trụ nêm). Ta thấy rằng đồ thị trông khá hợp lí và rất đẹp (khá gần với các giá trị tính toán từ bảng số liệu trên). Để tăng độ chính xác, ta có thể tăng số lượng dữ liệu trong bảng số liệu.
3. Kết luận
Việc dự đoán mực nước trong chiếc cốc cao vô hạn cứ ngỡ đơn giản, tuy nhiên việc tính toán lại rất phức tạp. Đặc biệt là tính toán thể tích của hình trụ nêm.
Tuy nhiên đây hoàn toàn là một nghiên cứu vấn đề thực tế rất hay, giúp học hỏi được các kĩ năng cần thiết trong việc nghiên cứu khoa học. Đồng thời vì đây là một vấn đề vật lý rất đơn giản, ta hoàn toàn có thể thực nghiệm và kiểm chứng kết quả với những gì mà ta vừa tính toán.